7 Efficient optimisation

Donald Knuth is a legendary American computer scientist who developed a number of the key algorithms that we use today (see for example ?Random). On the subject of optimisation he gives this advice:

The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature optimisation is the root of all evil (or at least most of it) in programming.

Knuth’s point is that it is easy to undertake code optimisation inefficiently. When developing code, the causes of inefficiencies may shift so that what originally caused slowness at the beginning of your work may not be relevant at a later stage. This means that time spent optimizing code early in the developmental stage could be wasted. Even worse, there is a trade-off between code speed and code readability; we’ve already made this trade-off once by using readable, (but slow) R compared with verbose C code!

For this reason this chapter is covered towards the latter half of the book. The previous chapters deliberately focussed on concepts, packages and functions to increase efficiency. These are (relatively) easy ways of saving time that, once implemented, will work for future projects. Code optimisation, by contrast, is an advanced topic that should only be tackled once ‘low hanging fruit’ for efficiency gains have been taken.

In this chapter we assume that you already have well-developed code that is mature conceptually and has been tried and tested. Now you want to optimize this code, but not prematurely. The chapter is organised as follows. First we begin with general hints and tips about optimising base R code. Code profiling can identify key bottlenecks in the code in need of optimisation, and this is covered in the next section. Section 7.5 discusses how parallel code can overcome efficiency bottlenecks for some problems. The final section explains how Rcpp can be used to efficiently incorporate C++ code into an R analysis.

Prerequisites

In this chapter, some of the examples require a working C++ compiler. The installation method depends on your operating system:

Linux: A compiler should already be installed. Otherwise, install r-base and a compiler will be installed as a dependency.
Macs: Install Xcode.
Windows: Install Rtools. Make sure you select the version that corresponds to your version of R.

The packages used in this chapter are

library("microbenchmark")
library("ggplot2movies")
library("profvis")
library("Rcpp")

7.1 Top 5 tips for efficient performance

Before you start to optimise your code, ensure you know where the bottleneck lies; use a code profiler.
If the data in your data frame is all of the same type, consider converting it to a matrix for a speed boost.
Use specialised row and column functions whenever possible.
The parallel package is ideal for Monte-Carlo simulations.
For optimal performance, consider re-writing key parts of your code in C++.

7.2 Code profiling

Often you will have working code, but simply want it to run faster. In some cases it’s obvious where the bottleneck lies. Sometimes you will guess, relying on intuition. A drawback of this is that you could be wrong, and waste time optimising the wrong piece of code. To make slow code run faster, it is first important to determine where the slow code lives. This is the purpose of code profiling.

The Rprof() function is a built-in tool for profiling the execution of R expressions. At regular time intervals, the profiler stops the R interpreter, records the current function call stack, and saves the information to a file. The results from Rprof() are stochastic. Each time we run a function in R, the conditions have changed. Hence, each time you profile your code, the result will be slightly different.

Unfortunately Rprof() is not user friendly. For this reason we recommend using the profvis package for profiling your R code. profvis provides an interactive graphical interface for visualising code profiling data data from Rprof().

7.2.1 Getting started with profvis

After installing profvis, e.g. with install.packages("profvis"), it can be used to profile R code. As a simple example, we will use the movies data set, which contains information on around 60,000 movies. First, we’ll select movies that are classed as comedies, then plot year the movie was made versus the movie rating, and draw a local polynomial regression line to pick out the trend. The main function from the profvis package is profvis(), which profiles the code and creates an interactive HTML page of the results. The first argument of profvis() is the R expression of interest. This can be many lines long:

library("profvis")
profvis({
  data(movies, package = "ggplot2movies") # Load data
  movies = movies[movies$Comedy == 1,]
  plot(movies$year, movies$rating)
  model = loess(rating ~ year, data = movies) # loess regression line
  j = order(movies$year)
  lines(movies$year[j], model$fitted[j]) # Add line to the plot
})

The above code provides an interactive HTML page (figure 7.1). On the left side is the code and on the right is a flame graph (horizontal direction is time in milliseconds and the vertical direction is the call stack).

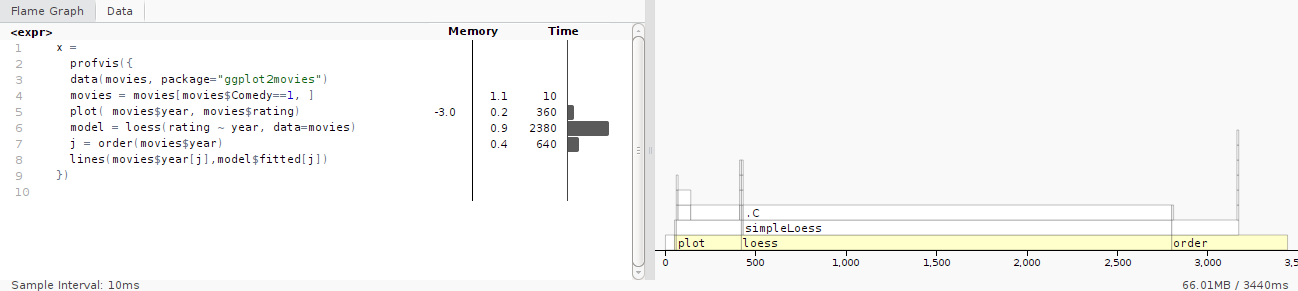
Figure 7.1: Output from profvis

The left hand panel gives the amount of time spent on each line of code. It shows that majority of time is spent calculating the loess() smoothing line. The bottom line of the right panel also highlights that most of the execution time is spent on the loess() function. Travelling up the function, we see that loess() calls simpleLoess() which in turn calls .C() function.

The conclusion from this graph is that if optimisation were required, it would make sense to focus on the loess() and possibly the order() function calls.

7.2.2 Example: Monopoly Simulation

Monopoly is a board game that originated in the United States over \(100\) years ago. The objective of the game is to go round the board and purchase squares (properties). If other players land on your properties they have to pay a tax. The player with the most money at the end of the game, wins. To make things more interesting, there are Chance and Community Chest squares. If you land on one of these squares, you draw card, which may send to you to other parts of the board. The other special square, is Jail. One way of entering Jail is to roll three successive doubles.

The efficient package contains a Monte-Carlo function for simulating a simplified game of monopoly. By keeping track of where a person lands when going round the board, we obtain an estimate of the probability of landing on a certain square. The entire code is around 100 lines long. In order for profvis to fully profile the code, the efficient package needs to be installed from source

devtools::install_github("csgillespie/efficient",
                         args = "--with-keep.source")

The function can then be profiled via the following code, which results in figure 7.2.

library("efficient")
profvis(simulate_monopoly(10000))

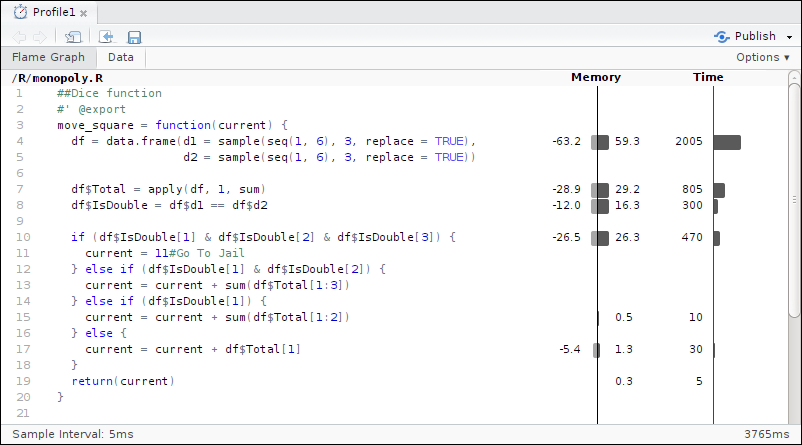
Figure 7.2: Code profiling for simulating the game of Monopoly.

The output from profvis shows that the vast majority of time (around 65%) is spent in the move_square() function.

In Monopoly moving around the board is complicated by the fact that rolling a double(a pair of 1’s, 2’s, …, 6’s) is special:

Roll two dice (total1): total_score = total1;
If you get a double, roll again (total2) and total_score = total1 + total2;
If you get a double, roll again (total3) and total_score = total1 + total2 + total3;
If roll three is a double, Go To Jail, otherwise move total_score.

The function move_square() captures this logic. Now we know where the code is slow, how can we speed up the computation? In the next section, we will discuss standard techniques that can be used. We will then revisit this example.

7.3 Efficient base R

In R there is often more than one way to solve a problem. In this section we highlight standard tricks or alternative methods that may improve performance.

The `if()` vs `ifelse()` functions

ifelse() is a vectorised version of the standard control-flow function if(test) if_yes else if_no that works as follows:

ifelse(test, if_yes, if_no)

In the above imaginary example, the return value is filled with elements from the if_yes and if_no arguments that are determined by whether the element of test is TRUE or FALSE. For example, suppose we have a vector of exam marks. ifelse() could be used to classify them as pass or fail:

marks = c(25, 55, 75)
ifelse(marks >= 40, "pass", "fail")
#> [1] "fail" "pass" "pass"

If the length of test condition is equal to \(1\), i.e. length(test) == 1, then the standard conditional statement

mark = 25
if(mark >= 40) {
  "pass" 
} else {
  "fail"
}

is around five to ten times faster than ifelse(mark >= 40, "pass", "fail").

An additional quirk of ifelse() is that although it is more programmer efficient, as it is more concise and understandable than multi-line alternatives, it is often less computationally efficient than a more verbose alternative. This is illustrated with the following benchmark, in which the second option runs around 20 times faster, despite the results being identical:

marks = runif(n = 10e6, min = 30, max = 99)
system.time({
  result1 = ifelse(marks >= 40, "pass", "fail")
})
#>    user  system elapsed 
#>   2.459   0.177   2.635
system.time({
  result2 = rep("fail", length(marks)) 
  result2[marks >= 40] = "pass"
})
#>    user  system elapsed 
#>   0.138   0.072   0.209
identical(result1, result2)
#> [1] TRUE

There is talk on the R-devel email list of speeding up ifelse() in base R. A simple solution is to use the if_else() function from dplyr, although, as discussed in the same thread, it cannot replace ifelse() in all situations. For our exam result test example, if_else() works fine and is much faster than base R’s implementation (although it is still around 3 times slower than the hard-coded solution):

system.time({
  result3 = dplyr::if_else(marks >= 40, "pass", "fail")
})
#>    user  system elapsed 
#>   0.453   0.180   0.633
identical(result1, result3)
#> [1] TRUE

Sorting and ordering

Sorting a vector is relatively quick; sorting a vector of length \(10^7\) takes around \(0.01\) seconds. If you only sort a vector once at the top of a script, then don’t worry too much about this. However if you are sorting inside a loop, or in a shiny application, then it can be worthwhile thinking about how to optimise this operation.

There are currently three sorting algorithms, c("shell", "quick", "radix") that can be specified in the sort() function; with radix being a new addition to R 3.3. Typically the radix (the non-default option) is the most computationally efficient option for most situations (it is around 20% faster when sorting a large vector of doubles).

Another useful trick is to partially order the results. For example, if you only want to display the top ten results, then use the partial argument, i.e. sort(x, partial = 1:10). For very large vectors, this can give a three fold speed increase.

Reversing elements

The rev() function provides a reversed version of its argument. If you wish to sort in decreasing order, sort(x, decreasing = TRUE) is marginally (around 10%) faster than rev(sort(x)).

Which indices are `TRUE`

To determine which index of a vector or array are TRUE, we would typically use the which() function. If we want to find the index of just the minimum or maximum value, i.e. which(x == min(x)) then using the efficient which.min()/which.max() variants can be orders of magnitude faster (see figure 7.3)

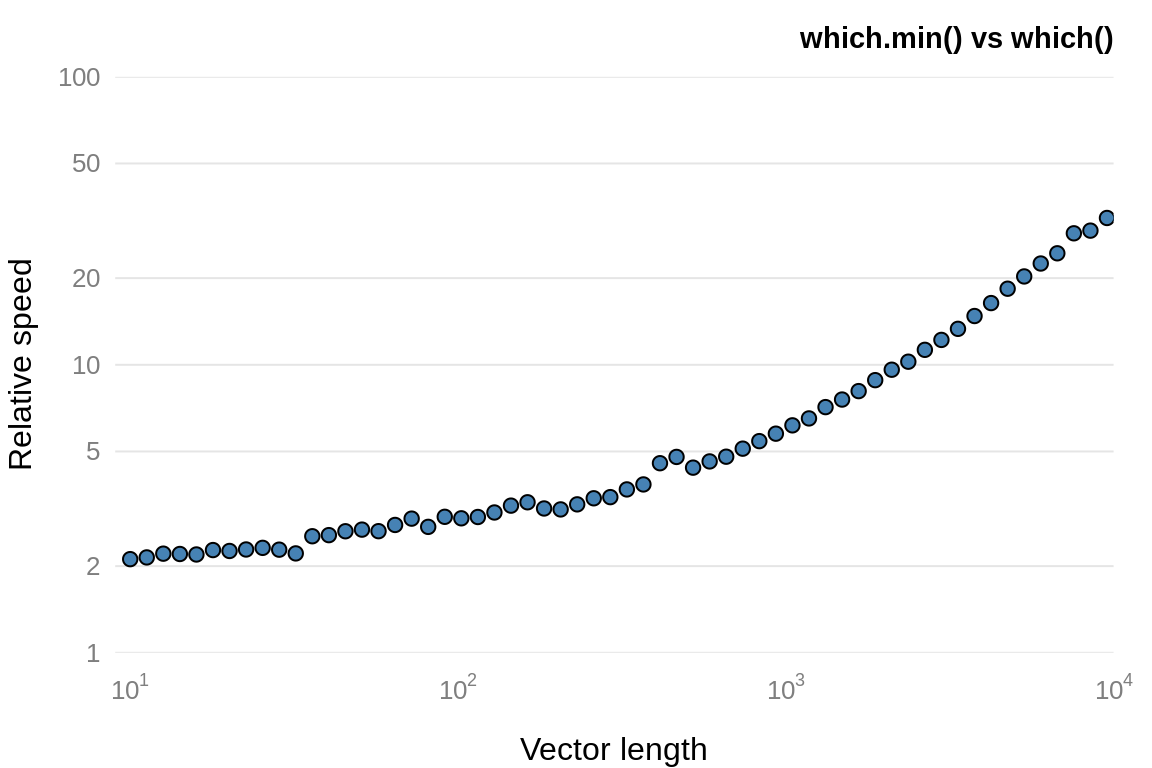
Figure 7.3: Comparison of which.min() with which().

Converting factors to numerics

A factor is just a vector of integers with associated levels. Occasionally we want to convert a factor into its numerical equivalent. The most efficient way of doing this (especially for long factors) is:

as.numeric(levels(f))[f]

Logical AND and OR

The logical AND (&) and OR (|) operators are vectorised functions and are typically used during multi-criteria subsetting operations. The code below, for example, returns TRUE for all elements of x less than \(0.4\) or greater than \(0.6\).

x < 0.4 | x > 0.6
#> [1]  TRUE FALSE  TRUE

When R executes the above comparison, it will always calculate x > 0.6 regardless of the value of x < 0.4. In contrast, the non-vectorised version, &&, only executes the second component if needed. This is efficient and leads to neater code, e.g.

# We only calculate the mean if data doesn't contain NAs
if(all(!is.na(x)) && mean(x) > 0) {
  # Do something
}

compared to

if(all(!is.na(x))) {
  if(mean(x) > 0) {
    # do somthing
  }
}

However care must be taken not to use && or || on vectors since it only evaluates the first element of the vector, giving the incorrect answer. This is illustrated below:

x < 0.4 || x > 0.6
#> [1] TRUE

Row and column operations

In data analysis we often want to apply a function to each column or row of a data set. For example, we might want to calculate the column or row sums. The apply() function makes this type of operation straightforward.

# Second argument: 1 -> rows. 2 -> columns
apply(data_set, 1, function_name)

There are optimised functions for calculating row and columns sums/means, rowSums(), colSums(), rowMeans() and colMeans() that should be used whenever possible. The package matrixStats contains many optimised row/col functions.

`is.na()` and `anyNA()`

To test whether a vector (or other object) contains missing values we use the is.na() function. Often we are interested in whether a vector contains any missing values. In this case, anyNA(x) is more efficient than any(is.na(x)).

Matrices

A matrix is similar to a data frame: it is a two dimensional object and sub-setting and other functions work in the same way. However all matrix elements must have the same type. Matrices tend to be used during statistical calculations. The lm() function, for example, internally converts the data to a matrix before calculating the results; any characters are thus recoded as numeric dummy variables.

Matrices are generally faster than data frames. For example, the datasets ex_mat and ex_df from the efficient package each have \(1000\) rows and \(100\) columns and contain the same random numbers. However selecting rows from the data frame is around \(150\) times slower than a matrix, as illustrated below:

data(ex_mat, ex_df, package="efficient")
microbenchmark(times=100, unit="ms", ex_mat[1,], ex_df[1,])
#> Unit: milliseconds
#>         expr    min     lq   mean  median      uq  max neval
#>  ex_mat[1, ] 0.0027 0.0034 0.0503 0.00424 0.00605 4.54   100
#>   ex_df[1, ] 0.4855 0.4974 0.5549 0.50535 0.51790 5.25   100

Use the data.matrix() function to efficiently convert a data frame into a matrix.

The integer data type

Numbers in R are usually stored in double-precision floating-point format, which is described in detail in Braun and Murdoch (2007) and Goldberg (1991). The term ‘double’ refers to the fact that on \(32\) bit systems (for which the format was developed) two memory locations are used to store a single number. Each double-precision number is accurate to around \(17\) decimal places.

When comparing floating point numbers we should be particularly careful, since y = sqrt(2) * sqrt(2) is not exactly \(2\), instead it’s almost \(2\). Using sprintf(“%.17f”, y) will give you the true value of y (to 17 decimal places).

Integers are another numeric data type. Integers primarily exist to be passed to C or Fortran code. You do not need to create integers for most applications. However, they are occasionally used to optimise sub-setting operations. When we subset a data frame or matrix, we are interacting with C code so we might be tempted to use integers with the purpose of speeding up our code. For example, if we look at the arguments for the head function

args(head.matrix)
#> function (x, n = 6L, ...) 
#> NULL

Using the : operator automatically creates a vector of integers.

we see that the default argument for n is 6L rather than simply 6 (the L is short for Literal and is used to create an integer). This gives a tiny speed boost (around 0.1 microseconds!)

x = runif(10)
microbenchmark(head(x, 6.0), head(x, 6L), times=1000000)
# Unit: microseconds
#        expr   min    lq  mean median    uq    max neval cld
#  head(x, 6) 7.067 8.309 9.058  8.686 9.098 105266 1e+06   a
# head(x, 6L) 6.947 8.219 8.933  8.594 9.007 106307 1e+06   a

Since this function is ubiquitous, this low level optimisation is useful. In general, if you are worried about shaving microseconds off your R code run time, you should probably consider switching to another language.

Integers are more space efficient. The code below compares the size of an integer vector to a standard numeric vector:

pryr::object_size(1:10000)
#> Registered S3 method overwritten by 'pryr':
#>   method      from
#>   print.bytes Rcpp
#> 40 kB
pryr::object_size(y = seq(1, 10000, by=1.0))
#> 80 kB

The results show that the integer version is roughly half the size. However, most mathematical operations will convert the integer vector into a standard numerical vector, as illustrated below:

is.integer(1L + 1)
#> [1] FALSE

Further storage savings can be obtained using the bit package.

Sparse matrices

Another data structure that can be stored efficiently is a sparse matrix. This is simply a matrix where most of the elements are zero. Conversely, if most elements are non-zero, the matrix is considered dense. The proportion of non-zero elements is called the sparsity. Large sparse matrices often crop up when performing numerical calculations. Typically, our data isn’t sparse but the resulting data structures we create may be sparse. There are a number of techniques/methods used to store sparse matrices. Methods for creating sparse matrices can be found in the Matrix package¹⁹.

As an example, suppose we have a large matrix where the diagonal elements are non-zero:

library("Matrix")
N = 10000
sp = sparseMatrix(1:N, 1:N, x = 1)
m = diag(1, N, N)

Both objects contain the same information, but the data is stored differently; since we have the same value multiple times in the matrix, we only need to store the value once and link it to multiple matrix locations. The matrix object stores each individual element, while the sparse matrix object only stores the location of the non-zero elements. This is much more memory efficient, as illustrated below:

pryr::object_size(sp)
#> 162 kB
pryr::object_size(m)
#> 800 MB

Exercises

Create a vector x. Benchmark any(is.na(x)) against anyNA(). Do the results vary with the size of the vector?
Examine the following function definitions to give you an idea of how integers are used. * tail.matrix() * lm().
Construct a matrix of integers and a matrix of numerics. Using pryr::object_size(), compare the objects.
How does the function seq.int(), which was used in the tail.matrix() function, differ to the standard seq() function?

A related memory saving idea is to replace logical vectors with vectors from the bit package which take up just over a 16th of the space (but you can’t use NAs).

7.4 Example: Optimising the `move_square()` function

Figure 7.2 shows that our main bottleneck in simulating the game of Monopoly is the move_square() function. Within this function, we spend around 50% of the time creating a data frame, 20% of the time calculating row sums, and the remainder on comparison operations. This piece of code can be optimised fairly easily (while still retaining the same overall structure) by incorporating the following improvements²⁰:

Instead of using seq(1, 6) to generate the 6 possible values of rolling a dice, use 1:6. Also, instead of a data frame, use a matrix and perform a single call to the sample() function
```
matrix(sample(1:6, 6, replace = TRUE), ncol = 2)
```
Overall, this revised line is around 25 times faster; most of the speed boost came from switching to a matrix.
Using rowSums() instead of apply(). The apply() function call is already faster since we’ve switched from a data frame to a matrix (around 3 times). Using rowSums() with a matrix, gives a 10 fold speed boost.
Use && in the if condition; this is around twice as fast compared to &.

Impressively the refactored code runs 20 times faster than the original code, compare figures 7.2 and 7.4, with the main speed boost coming from using a matrix instead of a data frame.

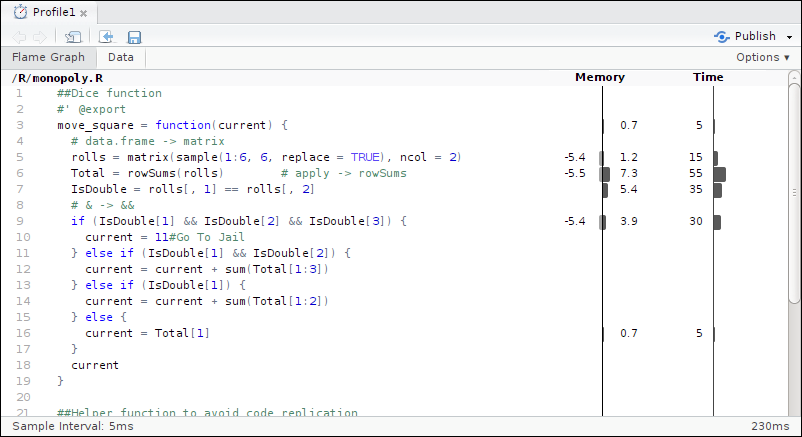
Figure 7.4: Code profiling of the optimised code.

Exercise

The move_square() function above uses a vectorised solution. Whenever we move, we always roll six dice, then examine the outcome and determine the number of doubles. However, this is potentially wasteful, since the probability of getting one double is \(1/6\) and two doubles is \(1/36\). Another method is too only roll additional dice if and when they are needed. Implement and time this solution.

7.5 Parallel computing

This section provides a brief foray into the world of parallel computing. It only looks at methods for parallel computing on ‘shared memory systems’. This simply means computers in which multiple central processor unit (CPU) cores can access the same block, i.e. most laptops and desktops sold worldwide. This section provides a flavour of what is possible; for a fuller account of parallel processing in R, see McCallum and Weston (2011).

The foundational package for parallel computing in R is parallel. In recent R versions (since R 2.14.0) this comes pre-installed with base R. The parallel package must still be loaded before use, however, and you must determine the number of available cores manually, as illustrated below:

library("parallel")
no_of_cores = detectCores()

The value returned by detectCores() turns out to be operating system and chip maker dependent - see help(“detectCores”) for full details. For most standard machines, detectCores() returns the number of simultaneous threads.

7.5.1 Parallel versions of apply functions

The most commonly used parallel applications are parallelised replacements of lapply(), sapply() and apply(). The parallel implementations and their arguments are shown below.

parLapply(cl, x, FUN, ...)
parApply(cl = NULL, X, MARGIN, FUN, ...)
parSapply(cl = NULL, X, FUN, ..., simplify = TRUE, USE.NAMES = TRUE)

The key point is that there is very little difference in arguments between parLapply() and lapply(), so the barrier to using (this form) of parallel computing is low, assuming you are proficient with the apply family of functions. Each function above has an argument cl, which is created by a makeCluster() call. This function, amongst other things, specifies the number of processors to use.

7.5.2 Example: Snakes and Ladders

Parallel computing is ideal for Monte-Carlo simulations. Each core independently simulates a realisation from the model. At the end, we gather up the results. In the efficient package, there is a function that simulates a single game of Snakes and Ladders - snakes_ladders()²¹

The following code illustrates how to simulate N games using sapply():

N = 10^4
sapply(1:N, snakes_ladders)

Rewriting this code to make use of the parallel package is straightforward. Begin by making a cluster object:

library("parallel")
cl = makeCluster(4)

Then simply swap sapply() for parSapply():

parSapply(cl, 1:N, snakes_ladders)

Not stopping the clusters can lead to memory leaks,²² so it is important to stop the created clusters as illustrated below:

stopCluster(cl)

and used a four (or more) core, then we would obtain a four-fold speed up (we set makeCluster(4)).

On a multi-processor computer with four (or more) cores, if we achieved perfect parallelisation this could lead to a four-fold speed-up. However, it is rare that we would achieve this optimal speed-up since there is always communication between threads.

7.5.3 Exit functions with care

Always call stopCluster() to free resources when you finish with the cluster object. However if the parallel code is within function, it’s possible that function ends as the results of an error and so stopCluster() is omitted.

The on.exit() function handles this problem with the minimum of fuss; regardless of how the function ends, on.exit() is always called. In the context of parallel programming we will have something similar to:

simulate = function(cores) {
  cl = makeCluster(cores)
  on.exit(stopCluster(cl))
  # Do something  
}

Another common use of on.exit() is with the par() function. If you use par() to change graphical parameters within a function, on.exit() ensures these parameters are reset to their previous value when the function ends.

7.5.4 Parallel code under Linux & OS X

If you are using Linux or OS X, then another way of running code in parallel is to use the mclapply() and mcmapply() functions

# This will run on Windows, but will only use 1 core
mclapply(1:N, snakes_ladders)

These functions use forking, that is creating a new copy of a process running on the CPU. However Windows does not support this low-level functionality in the way that Linux does. The main advantage of mclapply() is that you don’t have to start and stop cluster objects. The big disadvantage is that on Windows machines, you are limited to a single core.

7.6 Rcpp

Sometimes R is just slow. You’ve tried every trick you know, and your code is still crawling along. At this point you could consider rewriting key parts of your code in another, faster language. R has interfaces to other languages via packages, such as Rcpp, rJava, rPython and recently V8. These provide R interfaces to C++, Java, Python and JavaScript respectively. Rcpp is the most popular of these (figure 7.5).

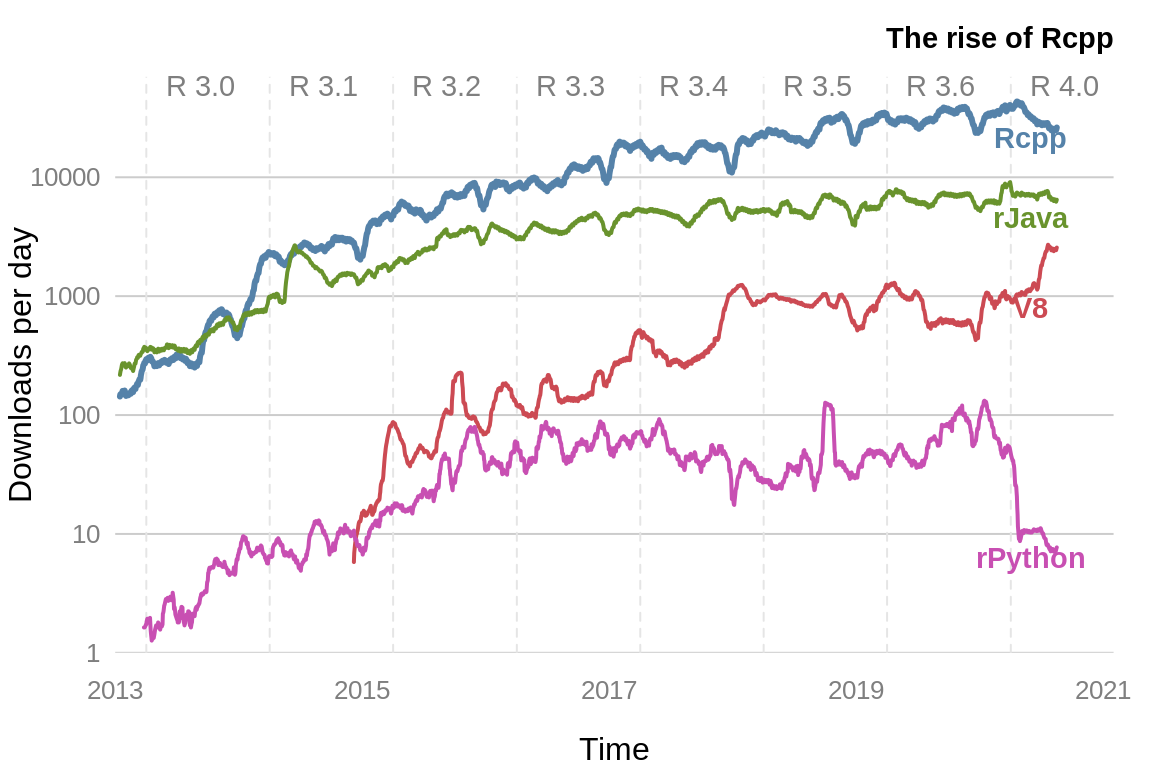
Figure 7.5: Downloads per day from the RStudio CRAN mirror of packages that provide R interfaces to other languages.

C++ is a modern, fast and very well-supported language with libraries for performing many kinds of computational tasks. Rcpp makes incorporating C++ code into your R workflow easy.

Although C/Fortran routines can be used using the .Call() function this is not recommended: using .Call() can be a painful experience. Rcpp provides a friendly API (Application Program Interface) that lets you write high-performance code, bypassing R’s tricky C API. Typical bottlenecks that C++ addresses are loops and recursive functions.

C++ is a powerful programming language about which entire books have been written. This section therefore is focussed on getting started and providing a flavour of what is possible. It is structured as follows. After ensuring that your computer is set-up for Rcpp, we proceed by creating a simple C++ function, to show how C++ compares with R (Section 7.6.1). This is converted into an R function using cppFunction() in Section 7.6.2. The remainder of the chapter explains C++ data types (Section 7.6.3), illustrates how to source C++ code directly (Section 7.6.4), explains vectors (Section 7.6.5) and Rcpp sugar (Section 7.6.6) and finally provides guidance on further resources on the subject (Section 7.6.7).

7.6.1 A simple C++ function

To write and compile C++ functions, you need a working C++ compiler (see the Prerequiste section at the beginning of this chapter). The code in this chapter was generated using version 1.0.6 of Rcpp.

Rcpp is well documented, as illustrated by the number of vignettes on the package’s CRAN page. In addition to its popularity, many other packages depend on Rcpp, which can be seen by looking at the Reverse Imports section.

To check that you have everything needed for this chapter, run the following piece of code from the course R package:

efficient::test_rcpp()

A C++ function is similar to an R function: you pass a set of inputs to the function, some code is run, a single object is returned. However there are some key differences.

In the C++ function each line must be terminated with ; In R, we use ; only when we have multiple statements on the same line.
We must declare object types in the C++ version. In particular we need to declare the types of the function arguments, return value and any intermediate objects we create.
The function must have an explicit return statement. Similar to R, there can be multiple returns, but the function will terminate when it hits it’s first return statement.
You do not use assignment when creating a function.
Object assignment must use = sign. The <- operator isn’t valid.
One line comments can be created using //. Multi-line comments are created using /*...*/

Suppose we want to create a function that adds two numbers together. In R this would be a simple one line affair:

add_r = function(x, y) x + y

In C++ it is a bit more long winded:

/* Return type double
 * Two arguments, also doubles
 */
double add_cpp(double x, double y) { 
  double value = x + y;
  return value;
}

If we were writing a C++ program we would also need another function called main(). We would then compile the code to obtain an executable. The executable is platform dependent. The beauty of using Rcpp is that it makes it very easy to call C++ functions from R and the user doesn’t have to worry about the platform, or compilers or the R/C++ interface.

7.6.2 The `cppFunction()` command

If we pass the C++ function created in the previous section as a text string argument to cppFunction():

library("Rcpp")
cppFunction('
  double add_cpp(double x, double y) {
    double value = x + y;
    return value;
  }
')

Rcpp will magically compile the C++ code and construct a function that bridges the gap between R and C++. After running the above code, we now have access to the add_cpp() function

add_cpp
#> function (x, y) 
#> .Call(<pointer: 0x7feb3c8ffb70>, x, y)

and can call the add_cpp() function in the usual way

add_cpp(1, 2)
#> [1] 3

We don’t have to worry about compilers. Also, if you include this function in a package, users don’t have to worry about any of the Rcpp magic. It just works.

7.6.3 C++ data types

The most basic type of variable is an integer, int. An int variable can store a value in the range \(-32768\) to \(+32767\). To store floating point numbers, there are single precision numbers, float and double precision numbers, double. A double takes twice as much memory as a float (in general, we should always work with double precision numbers unless we have a compelling reason to switch to floats). For single characters, we use the char data type.

There is also something called an unsigned int, which goes from \(0\) to \(65,535\) and a long int that ranges from \(0\) to \(2^{31}-1\).

Table 7.1: Overview of key C++ object types.
Type	Description
char	A single character.
int	An integer.
float	A single precision floating point number.
double	A double-precision floating point number.
void	A valueless quantity.

A pointer object is a variable that points to an area of memory that has been given a name. Pointers are a very powerful, but primitive facility contained in the C++ language. They are very useful since rather than passing large objects around, we pass a pointer to the memory location; rather than pass the house, we just give the address. We won’t use pointers in this chapter, but mention them for completeness. Table 7.1 gives an overview.

7.6.4 The `sourceCpp()` function

The cppFunction() is great for getting small examples up and running. But it is better practice to put your C++ code in a separate file (with file extension cpp) and use the function call sourceCpp("path/to/file.cpp") to compile them. However we need to include a few headers at the top of the file. The first line we add gives us access to the Rcpp functions. The file Rcpp.h contains a list of function and class definitions supplied by Rcpp. This file will be located where Rcpp is installed. The include line

#include <Rcpp.h>

causes the compiler to replace that lines with the contents of the named source file. This means that we can access the functions defined by Rcpp. To access the Rcpp functions we would have to type Rcpp::function_1. To avoid typing Rcpp::, we use the namespace facility

using namespace Rcpp;

Now we can just type function_1(); this is the same concept that R uses for managing function name collisions when loading packages. Above each function we want to export/use in R, we add the tag

// [[Rcpp::export]]

Similar to packages and the library() function in R, we access additional functions via #include. A standard header to include is #include <math.h> which contains standard mathematics functions.

This would give the complete file

#include <Rcpp.h>
using namespace Rcpp;

// [[Rcpp::export]]
double add_cpp(double x, double y) {
  double value = x + y;
  return value;
}

There are two main benefits with putting your C++ functions in separate files. First, we have the benefit of syntax highlighting (RStudio has great support for C++ editing). Second, it’s easier to make syntax errors when switching between R and C++ in the same file. To save space we’ll omit the headers for the remainder of the chapter.

7.6.5 Vectors and loops

Let’s now consider a slightly more complicated example. Here we want to write our own function that calculates the mean. This is just an illustrative example: R’s version is much better and more robust to scale differences in our data. For comparison, let’s create a corresponding R function - this is the same function we used in chapter 3. The function takes a single vector x as input, and returns the mean value, m:

mean_r = function(x) {
  m = 0
  n = length(x)
  for(i in 1:n)
    m = m + x[i] / n
  m
}

This is a very bad R function; we should just use the base function mean() for real world applications. However the purpose of mean_r() is to provide a comparison for the C++ version, which we will write in a similar way.

In this example, we will let Rcpp smooth the interface between C++ and R by using the NumericVector data type. This Rcpp data type mirrors the R vector object type. Other common classes are: IntegerVector, CharacterVector, and LogicalVector.

In the C++ version of the mean function, we specify the arguments types: x (NumericVector) and the return value (double). The C++ version of the mean() function is a few lines longer. Almost always, the corresponding C++ version will be, possibly much, longer. In general R optimises for reduced development time; C++ optimises for fast execution time. The corresponding C++ function for calculating the mean is:

double mean_cpp(NumericVector x) {
  int i;
  int n = x.size();
  double mean = 0;

  for(i = 0; i < n; i++) {
    mean = mean + x[i] / n;
  }
  return mean;
}

To use the C++ function we need to source the file (remember to put the necessary headers in).

sourceCpp("src/mean_cpp.cpp")

Although the C++ version is similar, there are a few crucial differences.

We use the .size() method to find the length of x.
The for loop has a more complicated syntax.
```
for (variable initialisation; condition; variable update ) {
  // Code to execute
}
```
In this example, the loop initialises i = 0 and will continue running until i < n is false. The statement i++ increases the value of i by 1; essentially it’s just shortcut for i = i + 1.
Similar to i++, C++ provides other operators to modify variables in place. For example we could rewrite part of the loop as
```
mean += x[i] / n;
```
The above code adds x[i] / n to the value of mean. Other similar operators are -=, *=, /= and i--.
A C++ vector starts at 0 not 1

To compare the C++ and R functions, we’ll generate some normal random numbers for the comparison:

x = rnorm(1e4)

Then call the microbenchmark() function (results plotted in figure 7.6).

# com_mean_r is the compiled version of mean_r
z = microbenchmark(
  mean(x), mean_r(x), com_mean_r(x), mean_cpp(x),
  times = 1000
)

In this simple example, the Rcpp variant is around \(100\) times faster than the corresponding pure R version. This sort of speed-up is not uncommon when switching to an Rcpp solution. Notice that the Rcpp version and standard base function mean() run at roughly the same speed; after all, the base R function is written in C. However, mean() uses a more sophisticated algorithm when calculating the mean to ensure accuracy.

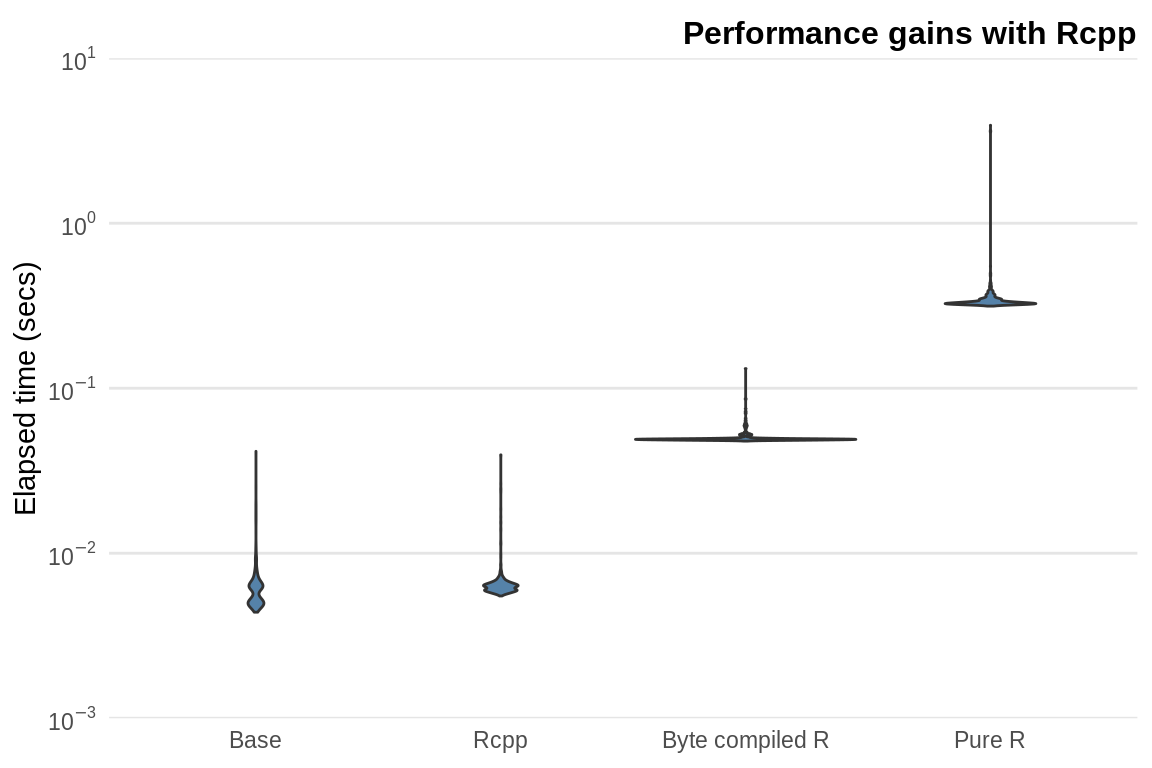
Figure 7.6: Comparison of mean functions.

Exercises

Consider the following piece of code:

double test1() {
  double a = 1.0 / 81;
  double b = 0;
  for (int i = 0; i < 729; ++i)
    b = b + a;
  return b;
}

Save the function test1() in a separate file. Make sure it works.
Write a similar function in R and compare the speed of the C++ and R versions.
Create a function called test2() where the double variables have been replaced by float. Do you still get the correct answer?
Change b = b + a to b += a to make your code more C++ like.
(Hard) What’s the difference between i++ and ++i?

Matrices

Each vector type has a corresponding matrix equivalent: NumericMatrix, IntegerMatrix, CharacterMatrix and LogicalMatrix. We use these types in a similar way to how we used NumericVector’s. The main differences are:

When we initialise, we need to specify the number of rows and columns

// 10 rows, 5 columns
NumericMatrix mat(10, 5);
// Length 10
NumericVector v(10);

We subset using (), i.e. mat(5, 4).
The first element in a matrix is mat(0, 0) - remember indexes start with 0 not 1.
To determine the number of rows and columns, we use the .nrow() and .ncol() methods.

7.6.6 C++ with sugar on top

Rcpp sugar brings a higher-level of abstraction to C++ code written using the Rcpp API. What this means in practice is that we can write C++ code in the style of R. For example, suppose we wanted to find the squared difference of two vectors; a squared residual in regression. In R we would use

sq_diff_r = function(x, y) (x - y)^2

Rewriting the function in standard C++ would give

NumericVector res_c(NumericVector x, NumericVector y) {
  int i;
  int n = x.size();
  NumericVector residuals(n);
  for(i = 0; i < n; i++) {
    residuals[i] = pow(x[i] - y[i], 2);
  }
  return residuals;
}

With Rcpp sugar we can rewrite this code to be more succinct and have more of an R feel:

NumericVector res_sugar(NumericVector x, NumericVector y) {
  return pow(x - y, 2);
}

In the above C++ code, the pow() function and x-y are valid due to Rcpp sugar. Other functions that are available include the d/q/p/r statistical functions, such as rnorm() and pnorm(). The sweetened versions aren’t usually faster than the C++ version, but typically there’s very little difference between the two. However with the sugared variety, the code is shorter and is constantly being improved.

Exercises

Construct an R version (using a for loop rather than the vectorised solution), res_r() and compare the three function variants.
In the above example, res_sugar() is faster than res_c(). Do you know why?

7.6.7 Rcpp resources

The aim of this section was to provide an introduction to Rcpp. One of the selling features of Rcpp is that there is a great deal of documentation available.

The Rcpp website;
The original Journal of Statistical Software paper describing Rcpp and the follow-up book (Eddelbuettel and François 2011; Eddelbuettel 2013);
H. Wickham (2014 a) provides a very readable chapter on Rcpp that goes into a bit more detail than this section;
The Rcpp section on the StackOverflow website. Questions are often answered by the Rcpp authors.

References

Braun, John, and Duncan J Murdoch. 2007. A First Course in Statistical Programming with R. Vol. 25. Cambridge University Press Cambridge.

Eddelbuettel, Dirk. 2013. Seamless R and C++ Integration with Rcpp. Springer.

Eddelbuettel, Dirk, and Romain François. 2011. “Rcpp: Seamless R and C++ Integration.” Journal of Statistical Software 40 (8): 1–18.

Goldberg, David. 1991. “What Every Computer Scientist Should Know About Floating-Point Arithmetic.” ACM Computing Surveys (CSUR) 23 (1): 5–48.

McCallum, Ethan, and Stephen Weston. 2011. Parallel R. O’Reilly Media.

Wickham, Hadley. 2014a. Advanced R. CRC Press.

Technically this isn’t in base R, it’s a recommended package.↩︎
Solutions are available in the efficient package vignette.↩︎
The idea for this example came to one of the authors after a particularly long and dull game of Snakes and Ladders with his son.↩︎
See github.com/npct/pct-shiny/issues/292 for a real world example of the dangers of not stopping created cores.↩︎

7 Efficient optimisation

Prerequisites

7.1 Top 5 tips for efficient performance

7.2 Code profiling

7.2.1 Getting started with profvis

7.2.2 Example: Monopoly Simulation

7.3 Efficient base R

The if() vs ifelse() functions

Sorting and ordering

Reversing elements

Which indices are TRUE

Converting factors to numerics

Logical AND and OR

Row and column operations

is.na() and anyNA()

Matrices

The integer data type

Sparse matrices

Exercises

7.4 Example: Optimising the move_square() function

Exercise

7.5 Parallel computing

7.5.1 Parallel versions of apply functions

7.5.2 Example: Snakes and Ladders

7.5.3 Exit functions with care

7.5.4 Parallel code under Linux & OS X

7.6 Rcpp

7.6.1 A simple C++ function

7.6.2 The cppFunction() command

7.6.3 C++ data types

7.6.4 The sourceCpp() function

7.6.5 Vectors and loops

Exercises

Matrices

7.6.6 C++ with sugar on top

Exercises

7.6.7 Rcpp resources

References

The `if()` vs `ifelse()` functions

Which indices are `TRUE`

`is.na()` and `anyNA()`

7.4 Example: Optimising the `move_square()` function

7.6.2 The `cppFunction()` command

7.6.4 The `sourceCpp()` function