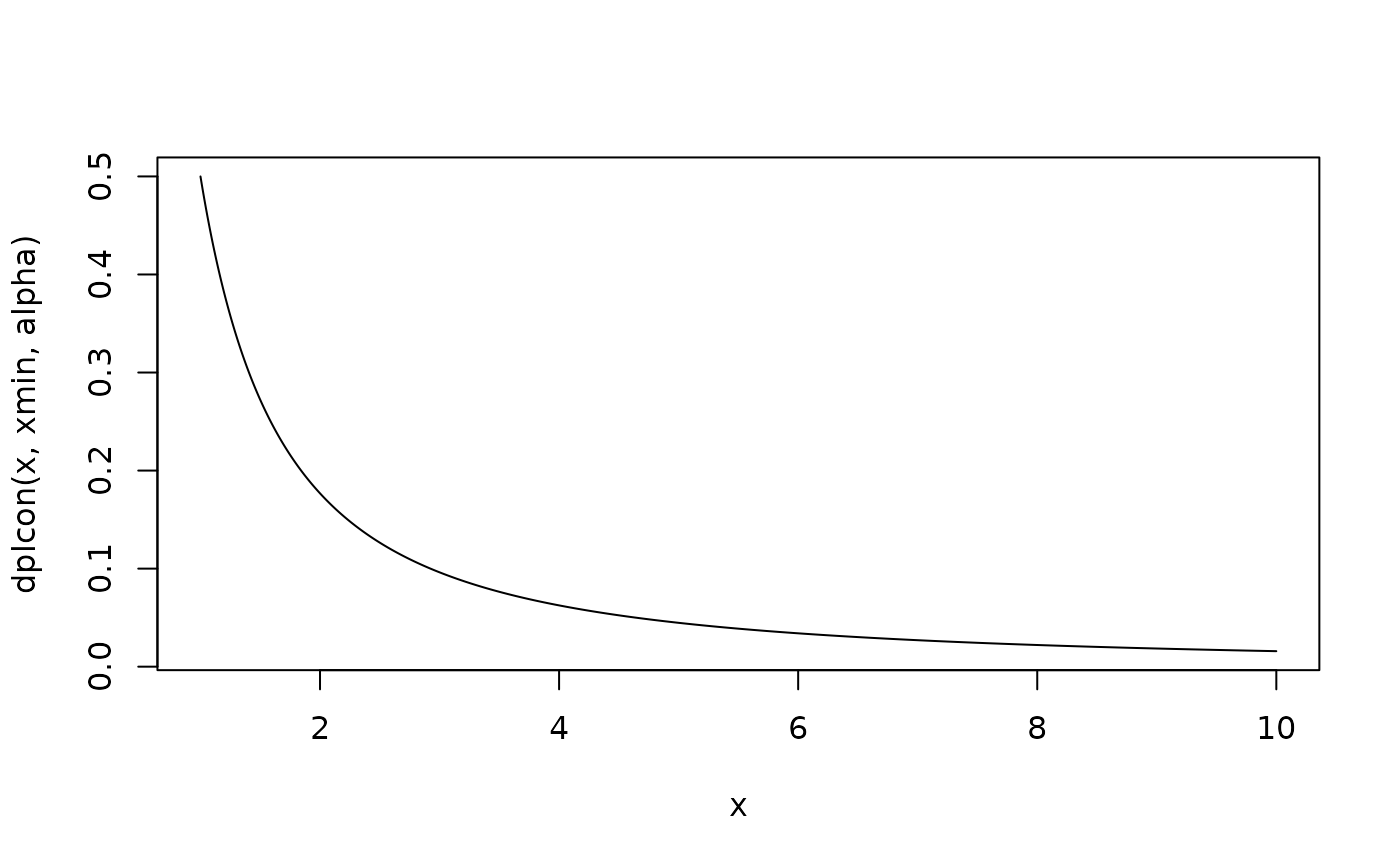
Density and distribution function of the continuous power-law distribution, with parameters xmin and alpha.
Usage
dplcon(x, xmin, alpha, log = FALSE)
pplcon(q, xmin, alpha, lower.tail = TRUE)
rplcon(n, xmin, alpha)Arguments
- x, q
vector of quantiles. The discrete power-law distribution is defined for
x > xmin- xmin
The lower bound of the power-law distribution. For the continuous power-law, xmin >= 0. for the discrete distribution, xmin > 0.
- alpha
The scaling parameter: alpha > 1.
- log
logical (default FALSE) if TRUE, log values are returned.
- lower.tail
logical; if TRUE (default), probabilities are \(P[X \le x]\), otherwise, \(P[X > x]\).
- n
Number of observations. If
length(n) > 1, the length is taken to be the number required.
Examples
xmin = 1; alpha = 1.5
x = seq(xmin, 10, length.out=1000)
plot(x, dplcon(x, xmin, alpha), type="l")
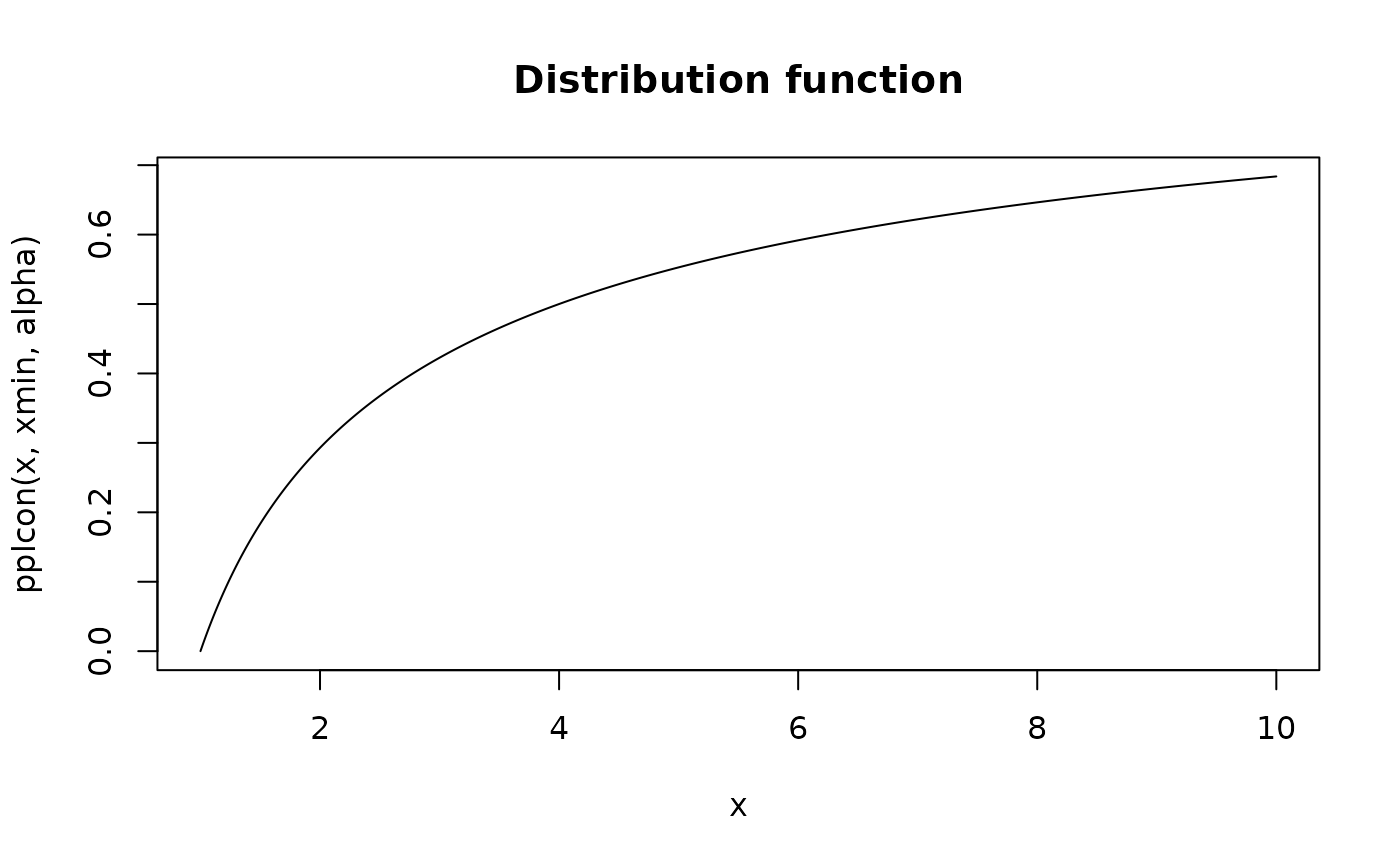
 plot(x, pplcon(x, xmin, alpha), type="l", main="Distribution function")
plot(x, pplcon(x, xmin, alpha), type="l", main="Distribution function")
 n = 1000
con_rns = rplcon(n, xmin, alpha)
con_rns = sort(con_rns)
p = rep(1/n, n)
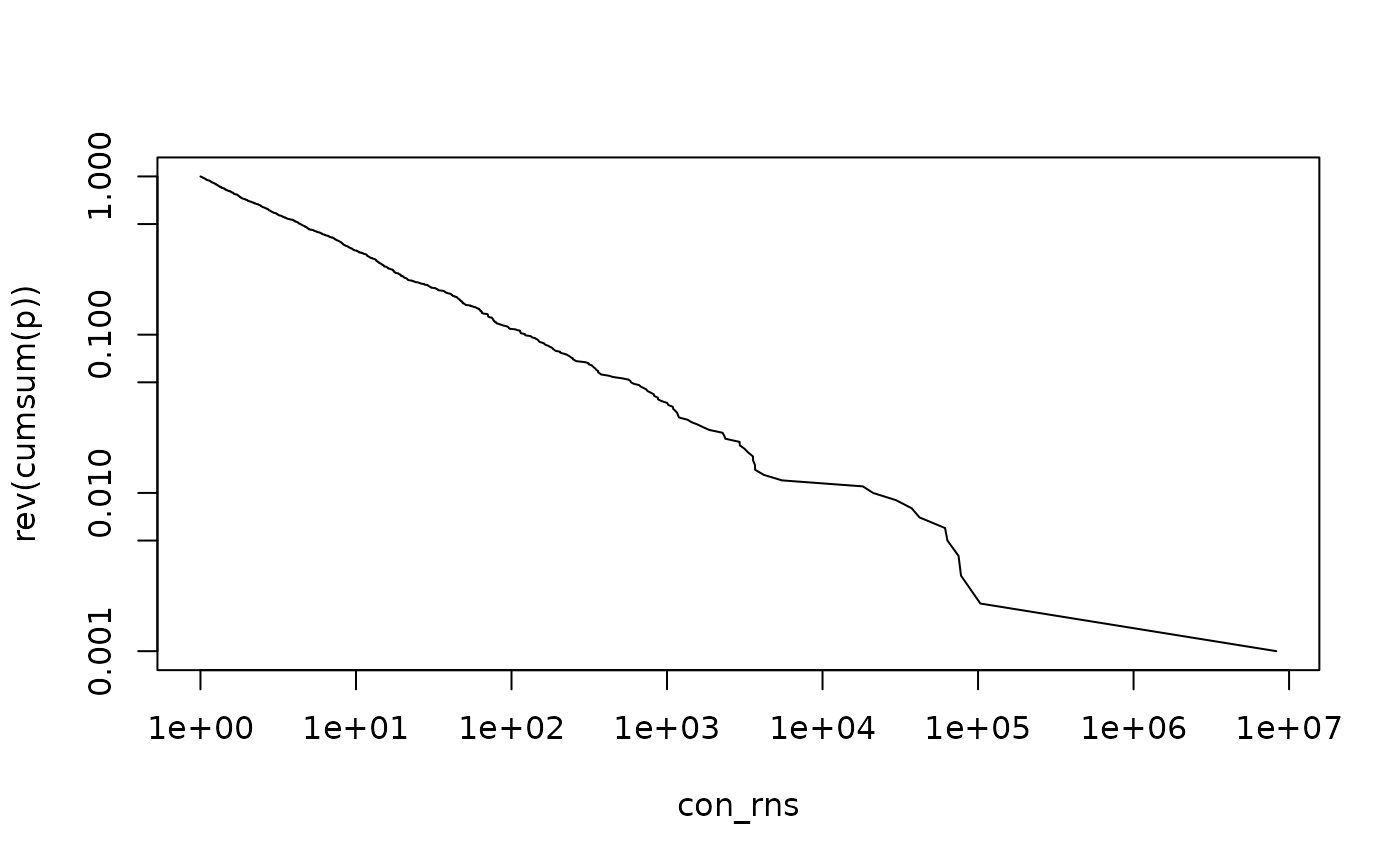
#Zipfs plot
plot(con_rns, rev(cumsum(p)), log="xy", type="l")
n = 1000
con_rns = rplcon(n, xmin, alpha)
con_rns = sort(con_rns)
p = rep(1/n, n)
#Zipfs plot
plot(con_rns, rev(cumsum(p)), log="xy", type="l")