Vuong's test for non-nested models

Since it is possible to fit power law models to any data set, it is recommended that alternative distributions are considered. A standard technique is to use Vuong's test. This is a likelihood ratio test for model selection using the Kullback-Leibler criteria. The test statistic, R, is the ratio of the log-likelihoods of the data between the two competing models. The sign of R indicates which model is better. Since the value of R is estimated, we use the method proposed by Vuong, 1989 to select the model.

Usage

compare_distributions(d1, d2)

Arguments

d1

A distribution object

d2

A distribution object

Value

This function returns

test_statistic

The test statistic.

p_one_sided

A one-sided p-value, which is an upper limit on getting that small a log-likelihood ratio if the first distribution, d1, is actually true.

p_two_sided

A two-sided p-value, which is the probability of getting a log-likelihood ratio which deviates that much from zero in either direction, if the two distributions are actually equally good.

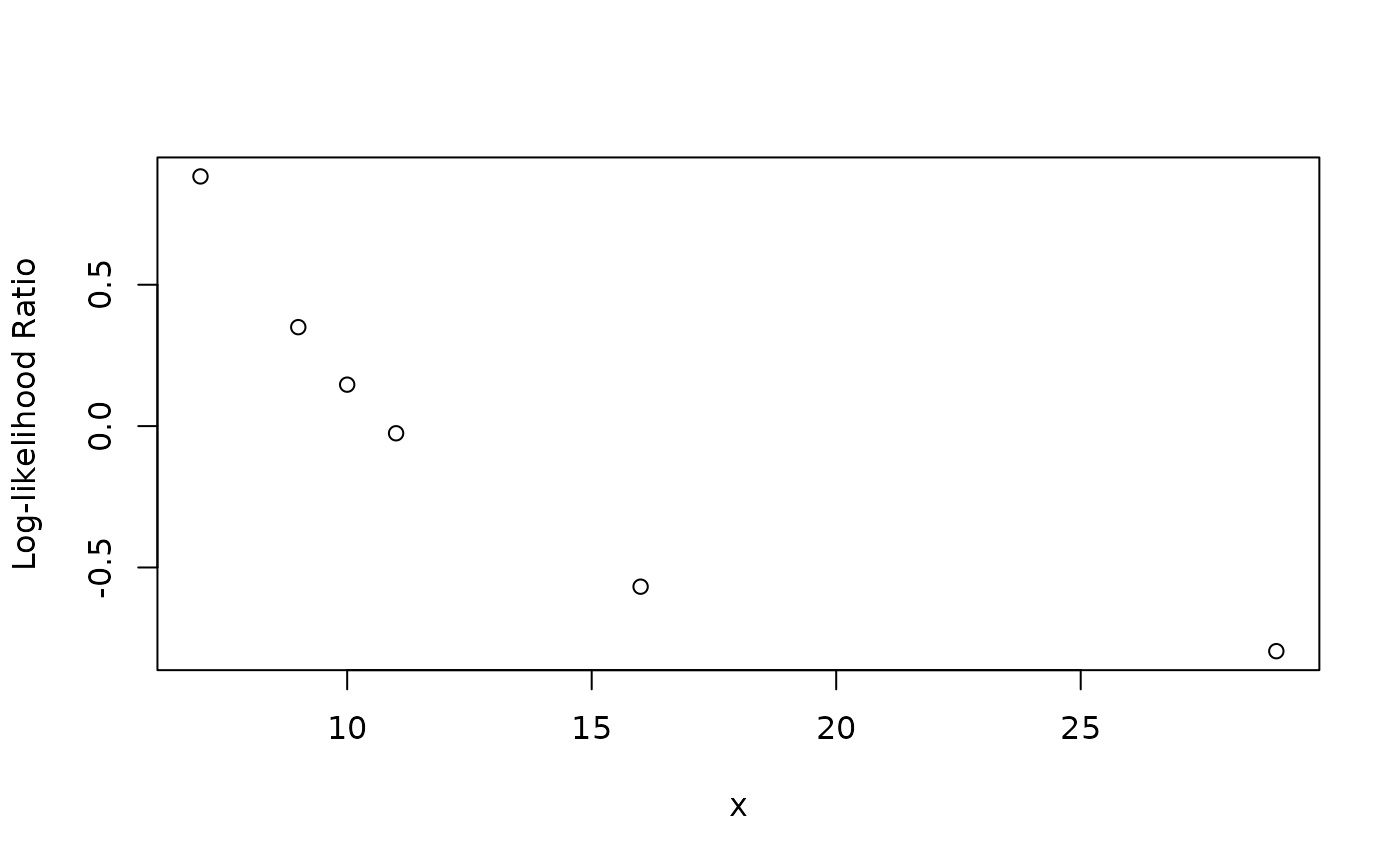
ratio

A data frame with two columns. The first column is the x value and second column is the difference in log-likelihoods.

Details

This function compares two models. The null hypothesis is that both classes of distributions are equally far from the true distribution. If this is true, the log-likelihood ratio should (asymptotically) have a Normal distribution with mean zero. The test statistic is the sample average of the log-likelihood ratio, standardized by a consistent estimate of its standard deviation. If the null hypothesis is false, and one class of distributions is closer to the "truth", the test statistic goes to +/-infinity with probability 1, indicating the better-fitting class of distributions.

Note

Code initially based on R code developed by Cosma Rohilla Shalizi (http://bactra.org/). Also see Appendix C in Clauset et al, 2009.

References

Vuong, Quang H. (1989): "Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses", Econometrica 57: 307–333.

Examples

########################################################
# Example data                                         #
########################################################
x = rpldis(100, xmin=2, alpha=3)

########################################################
##Continuous power law                                 #
########################################################
m1 = conpl$new(x)
m1$setXmin(estimate_xmin(m1))

########################################################
##Exponential
########################################################
m2 = conexp$new(x)
m2$setXmin(m1$getXmin())
est2 = estimate_pars(m2)
m2$setPars(est2$pars)

########################################################
##Vuong's test                                         #
########################################################
comp = compare_distributions(m1, m2)
plot(comp)